Last active
December 6, 2024 16:54
-
Star
(180)
You must be signed in to star a gist -
Fork
(11)
You must be signed in to fork a gist
-
-
Save rxwei/30ba75ce092ab3b0dce4bde1fc2c9f1d to your computer and use it in GitHub Desktop.
Revisions
-
rxwei revised this gist
Nov 4, 2019 . 1 changed file with 1 addition and 2056 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -1,2056 +1 @@ ### See the official [Differentiable Programming Manifesto](https://github.com/apple/swift/tree/master/docs/DifferentiableProgramming.md) instead. -
rxwei revised this gist
Jun 17, 2019 . 1 changed file with 1 addition and 1 deletion.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -9,7 +9,7 @@ programming language design community, with a strong focus on language design. **Status: Outdated** **Please see [Swift Automatic Differentiation Design Overview](https://docs.google.com/document/d/1bPepWLfRQa6CtXqKA8CDQ87uZHixNav-TFjLSisuKag/edit?usp=sharing) instead.** ## Table of Contents -
rxwei revised this gist
Jun 17, 2019 . 1 changed file with 3 additions and 1 deletion.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -7,7 +7,9 @@ First-Class Automatic Differentiation in Swift: A Manifesto This document is written for both the machine learning community and the Swift programming language design community, with a strong focus on language design. **Status: Outdated** Please see [Swift Automatic Differentiation Design Overview] instead. ## Table of Contents -
rxwei revised this gist
Dec 5, 2018 . 1 changed file with 1 addition and 1 deletion.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -7,7 +7,7 @@ First-Class Automatic Differentiation in Swift: A Manifesto This document is written for both the machine learning community and the Swift programming language design community, with a strong focus on language design. **Status: Currently undergoing major revision.** ## Table of Contents -
rxwei revised this gist
Nov 12, 2018 . 1 changed file with 2 additions and 0 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -7,6 +7,8 @@ First-Class Automatic Differentiation in Swift: A Manifesto This document is written for both the machine learning community and the Swift programming language design community, with a strong focus on language design. Status: Currently undergoing major revision. ## Table of Contents - [Introduction](#introduction) -
rxwei revised this gist
Oct 29, 2018 . 2 changed files with 0 additions and 68 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -1,3 +0,0 @@ This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -1,65 +0,0 @@ -
rxwei revised this gist
Oct 29, 2018 . 2 changed files with 68 additions and 0 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -0,0 +1,3 @@ *.tex *.pdf auto/ This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -0,0 +1,65 @@ #+TITLE: The Reduced Differentiability Model #+SUBTITLE: Using only Differentials and Adjoints * TODO Introduction * TODO Motivation * Solution ** Rule of First-Order Differentiability * A function is forward-differentiable if * it has a forward-differentiable body, * it has a differential, or * it has a reverse-differentiable /adjoint/. * A function is reverse-differentiable if * it has a reverse-differentiable body, * it has a reverse-differentiable /differential/, or * it has an /adjoint/. ** TODO Rule of Higher-Order Differentiability ** Simplified Differential and Adjoint Definition Syntax #+BEGIN_SRC swift extension Vector { @differentiable(wrt: self) static func * (lhs: Vector, rhs: Vector) -> Vector { return ... // non-differentiable adjoint(v: Vector) -> (Vector, Vector) { return (rhs * v, lhs * v) } } } #+END_SRC #+BEGIN_SRC swift @differentiable func cos(_ x: Vector) -> Vector { return ... // non-differentiable differential(v: Vector) -> Vector { return -sin(x) * v } } #+END_SRC #+BEGIN_SRC swift extension Tensor { @differentiable(wrt: self) func transposed() -> Tensor { return ... // non-differentiable adjoint(v: Tensor) -> Tensor { return v.transposed() } } } #+END_SRC -
rxwei revised this gist
Oct 23, 2018 . 1 changed file with 12 additions and 11 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -83,23 +83,24 @@ func f(_ x: Double, _ y: Double) -> Double { ### Vectors and Jacobians In numerical computing, users often write code that operates on high-dimensional mathematical objects. The basic typing rules that we defined on real scalars (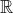) can be generalized for [module](https://en.wikipedia.org/wiki/Module_(mathematics))-like types such as vectors with extra consideration for shape. In vector calculus, the differentiation of a function  is defined per scalar because there are multiple inputs and multiple outputs. Full differentiation of a vector-valued function  will thus result in a matrix, each of whose entries is a function that computes the partial derivative of an output scalar with respect to an input scalar. This matrix is called a [Jacobian](https://en.wikipedia.org/wiki/Jacobian_matrix_and_determinant). In this definition, the Jacobian matrix has type ^{mn}). For simplicity, we will model it as a function that maps vectors to real-valued matrices . <p align="center"> <img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/74e93aa903c2695e45770030453eb77224104ee4" @@ -118,7 +119,7 @@ func 𝒟<T>(_ f: (Vector2<T>) -> Vector3<T>) -> (Vector2<T>) -> Matrix3x2<T> Computing the Jacobian of a function is often unnecessary in gradient-based optimization methods. Computing a full Jacobian will require repeated evaluations of some primitives in computer code: vector-Jacobian products (VJPs) or Jacobian-vector products (JVPs), and VJPs and JVPs are often exactly what we need in practice. In these terms, "vector" refers to a vector of partial derivatives that are to be chained with the Jacobian by left-multiplication or right-multiplication. As we explain chaining next, we discuss how Automatic @@ -1044,7 +1045,7 @@ and function convert back and forth through conversion thunks implicitly. ```swift // A "thin" function that captures no variables. // Its representation is `@convention(thin)` by default. func f(x: Int) -> Int { return x } -
rxwei revised this gist
Oct 23, 2018 . 1 changed file with 1 addition and 1 deletion.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -477,7 +477,7 @@ multiplication). The protocol will be called `Arithmetic`. ```swift public protocol Arithmetic: Equatable { static var zero: Self { get } prefix static func + (x: Self) -> Self static func + (lhs: Self, rhs: Self) -> Self static func += (lhs: inout Self, rhs: Self) -> Self -
rxwei revised this gist
Oct 23, 2018 . 1 changed file with 7 additions and 6 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -115,13 +115,14 @@ func 𝒟<T>(_ f: (Vector2<T>) -> Vector3<T>) -> (Vector2<T>) -> Matrix3x2<T> where T: FloatingPoint ``` Computing the Jacobian of a function is often unnecessary in gradient-based optimization methods. Computing a full Jacobian will require repeated evaluations of some primitives in computer code: vector-Jacobian products (VJPs) and Jacobian-vector products (JVPs), and VJPs and JVPs are often exactly what we need in practice. In these terms, "vector" refers to a vector of partial derivatives that are to be chained with the Jacobian by left-multiplication or right-multiplication. As we explain chaining next, we discuss how Automatic Differentiation comes in the picture. ### Gradient and Reverse-Mode AD -
rxwei revised this gist
Oct 23, 2018 . 1 changed file with 16 additions and 17 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -116,12 +116,12 @@ func 𝒟<T>(_ f: (Vector2<T>) -> Vector3<T>) -> (Vector2<T>) -> Matrix3x2<T> ``` Calculating the Jacobian of a function is often unnecessary in gradient-based optimization methods. Computing a full Jacobian will require repeated evaluations of vector-Jacobian products (VJPs) and Jacobian-vector products (JVPs), but VJPs and JVPs are often what we need in practice. In these terms, "vector" refers to a vector of partial derivatives that are to be chained with the Jacobian by left-multiplication or right-multiplication. As we explain chaining next, we discuss how Automatic Differentiation comes in the picture. ### Gradient and Reverse-Mode AD @@ -469,10 +469,10 @@ On the Swift forum, we have discussed the [fundamental blocker for vector types to conform to the existing `Numeric` protocol](https://forums.swift.org/t/should-numeric-not-refine-expressiblebyintegerliteral). The consensus was to introduce a weakening of the `Numeric` protocol to represent the abstractions shared between scalars and vectors: [rng (ring without unity)](https://en.wikipedia.org/wiki/Rng_(algebra)) (We assumed that vector spaces are rngs by endowing them with `*` as element-wise multiplication). The protocol will be called `Arithmetic`. ```swift public protocol Arithmetic: Equatable { @@ -502,13 +502,12 @@ public protocol Numeric: Arithmetic, ExpressibleByIntegerLiteral { After we introduce the `Arithmetic` protocol, which makes the standard library suitable for vector APIs and beyond, we can define a protocol that generalizes vectors. Mathematically, a vector space is a ring without unity if we endow them with `*` as element-wise multiplication. We represent vector spaces through the `VectorNumeric` protocol as follows. `Scalar` is the type of the elements of this vector space -- the field which the vector space is over. `Shape` is the shape of this vector space, which is customizable. The initializer takes a value of the `Scalar` type and a `Shape` and returns a vector of the specified shape. ```swift /// A type that represents an unranked vector space. Values of this type are -
rxwei revised this gist
Oct 22, 2018 . 1 changed file with 1 addition and 1 deletion.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -390,7 +390,7 @@ func hvp<T: Differentiable, R: FloatingPoint>( By building first-class AD into the programming language, we can provide better diagnostics about differentiability and numeric stability than any other dynamic languages, all at compile-time. ```console test.swift:58:10: error: function is not differentiable -
rxwei revised this gist
Oct 22, 2018 . 1 changed file with 5 additions and 4 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -675,8 +675,6 @@ There are five options for differentiability: 2. Reverse: `@differentiable(reverse, adjoint: ...)` This option says that the function is reverse-mode differentiable. Reverse-mode differentiation requires the "adjoint code" (or adjoint function) of this function, so that Swift knows how to compute the function's @@ -697,7 +695,7 @@ There are five options for differentiability: By definition, constant functions always have zero derivatives and are differentiable at any arbitrary order. So differentiating this function will result into a zero vector (or vectors, when the function has multiple differentiation arguments) with the same shape as each differentiation argument. @@ -885,7 +883,10 @@ expression = autodiff-expression Gradient and derivatives are two special cases of differentiation where the output or the result is a scalar, respectively. When they are not a scalar, vector-Jacobian products and Jacobian-vector products are being computed with a vector. These cases are not obvious, but are required for modular machine learning APIs where each neural network layer defines a back-propagation method that takes a partial derivative vector back-propagated from the previous layer. As such, we add two extra differential operators which will be useful for computing these products. - `#differential(f)`: Produces a function that takes the original arguments and -
rxwei revised this gist
Oct 21, 2018 . 1 changed file with 2 additions and 2 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -1242,8 +1242,8 @@ type, forming a "normal" function. This allows us to define generic algorithms using differentiation, without specializing them on function types of each differentiability. The following table shows whether each differentiability (as a column label) can be converted to another (as a row label). | Convertible to: | None | Linear | Constant | Forward | Reverse | Bidirectional | |-----------------|------|-----------|----------|---------|---------|---------------| -
rxwei revised this gist
Oct 21, 2018 . 1 changed file with 3 additions and 2 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -882,11 +882,12 @@ expression = autodiff-expression ### Embrace Generality: Vector-Jacobian Products and Jacobian-Vector Products Gradient and derivatives are two special cases of differentiation where the output or the result is a scalar, respectively. When they are not a scalar, vector-Jacobian products and Jacobian-vector products are being computed with a vector. We add two extra differential operators which will be useful for computing these products. - `#differential(f)`: Produces a function that takes the original arguments and returns the differential of `f`. - `#pullback(f)`: Produces a function that takes the original arguments and -
rxwei revised this gist
Oct 21, 2018 . 1 changed file with 8 additions and 7 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -116,9 +116,8 @@ func 𝒟<T>(_ f: (Vector2<T>) -> Vector3<T>) -> (Vector2<T>) -> Matrix3x2<T> ``` Calculating the Jacobian of a function is often unnecessary in gradient-based optimization methods. In practice, we care more about two byproducts of Jacobian calculation that are significantly easier to compute than the Jacobian itself: vector-Jacobian products and Jacobian-vector products. In these terms, "vector" refers to a vector of partial derivatives that are to be chained with the Jacobian by left-multiplication or right-multiplication. As we explain chaining @@ -140,11 +139,13 @@ row in the matrix, which is exactly the <img src="https://latex.codecogs.com/gif.latex?\nabla{f_i}(\mathbf{x})=\mathbf{v}^i\mathbf{J_f}(\mathbf{x})=\bigg[\dfrac{\partial{f_i}(\mathbf{x})}{\partial&space;x_1}&space;\&space;\cdots&space;\&space;\dfrac{\partial{f_i}(\mathbf{x})}{\partial{x_n}}\bigg]" title="\nabla{f_i}(\mathbf{x})=\mathbf{v}^i\mathbf{J_f}(\mathbf{x})=\bigg[\dfrac{\partial{f_i}(\mathbf{x})}{\partial x_1} \ \cdots \ \dfrac{\partial{f_i}(\mathbf{x})}{\partial{x_n}}\bigg]" /> </p> When vector  in ) represents the gradient of another function  at ), namely }), then the vector-Jacobian products represents . The linear function that takes a vector and left-multiplies it with the Jacobian is also called a @@ -514,7 +515,7 @@ customizable. The initializer takes a value of the `Scalar` type and a /// elements in this vector space and with a specific shape. public protocol VectorNumeric: Arithmetic { /// The type of scalars in the vector space. associatedtype Scalar: Numeric /// The type whose values specifies the shape of an object in the vector /// space. -
rxwei revised this gist
Oct 21, 2018 . 1 changed file with 1 addition and 1 deletion.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -89,7 +89,7 @@ mathematical objects. The basic typing rules that we defined on real scalars [module](https://en.wikipedia.org/wiki/Module_(mathematics))-like types such as vectors with extra consideration for shape. In vector calculus, the differentiation of a function  is defined per scalar because there are multiple inputs and multiple outputs. Full differentiation of vector-valued function  will result in a matrix, -
rxwei revised this gist
Oct 21, 2018 . 1 changed file with 2 additions and 2 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -2044,5 +2044,5 @@ for _ in 0...5 { The author would like to thank Dan Zheng, Chris Lattner, Alex Wiltschko, Bart van Merriënboer, Gordon Plotkin, Dougal Maclaurin, Matthew Johnson, Casey Chu, Tim Harley, Marc Rasi, and Dmitri Gribenko for their input to the initial design of this powerful language feature. -
rxwei revised this gist
Oct 21, 2018 . 1 changed file with 33 additions and 16 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -324,10 +324,10 @@ for (x, y) in minibatches { We want our AD system to be fully extensible to the point where users can request derivatives of a function taking their own user-defined numeric types, and even use this feature to implement structure-dependent algorithms such as tree-recursive neural networks. Therefore, when performing AD, Swift makes no special assumptions about individual math functions or the types it should support. We enable library designers and developers to easily define any type or differentiable functions, all in pure Swift code. Swift supports [protocol-oriented programming and first-class value semantics](https://developer.apple.com/videos/play/wwdc2015/408/). AD is deeply @@ -341,8 +341,10 @@ extension MyType: Differentiable { } ``` Or make an obviously non-differentiable function differentiable by using the `@differentiable` attribute, specifying a "tangent" function for computing its Jacobian-vector products, or an "adjoint" function for computing its vector-Jacobian products. ```swift @differentiable(tangent: tangentFoo, adjoint: adjointFoo) @@ -377,9 +379,8 @@ trigger differentiation as needed. ```swift func hvp<T: Differentiable, R: FloatingPoint>( at x: T, in f: @autodiff(order: 2) (T) -> R ) -> @autodiff(linear) (T) -> T { return differential(at: x, in: gradient(of: f)) } ``` @@ -416,16 +417,31 @@ imperative. | | Syntax | Meaning | |------------|--------|-------------| | Functional | `let 𝝯f = gradient(of: f)`<br/>`𝝯f(x)` | Differentiating a function | | Imperative | `let y = f(x)`<br/>`gradient(of: y, wrt: x)` | Differentiating code traced through data flow | Functional-style AD is transforming one function to another, producing a function that takes original arguments and returns the partial derivatives evaluated at each argument. Imperative-style AD, on the other hand, is a value-value dependency analysis. Although we use both notations in mathematics, imperative AD comes at the cost of semantic inconsistency with the host language, for example: ```swift let y = f(x) x = 3 gradient(of: y, wrt: x) // undefined ``` Semantically, `y` is a value, but `x` is both a value and a reference to a memory location -- it is unclear what exactly we are differentiating with respect to. Though making `y` and `x` have reference types could make this particular example work out semantically, it would be fundamentally inconsistent with Swift's core design where mathematical objects have value types, and would also make scalar types like `Float` incompatible with automatic differentiation. We believe Swift's AD can achieve the same level of expressivity as imperative AD while preserving functional properties, and use language integration to push developers' productivity to the next level. ## Part 1: Differentiable Types @@ -559,8 +575,9 @@ based on: As such we provide a syntactic way of specifying the differentiability of a function, using either the function's linearity properties or a separate function to specify the "tangent code", which specifies how to differentiate the function in forward mode, or "adjoint code”, which specifies how to differentiate the function in reverse mode. ### The `@differentiable` attribute @@ -622,7 +639,7 @@ public func conv2d(_ input: Tensor<Float>, filter: Tensor<Float>, func adjointConv2D(_ input: Tensor<Float>, filter: Tensor<Float>, strides: (Int32, Int32, Int32, Int32), padding: Padding) -> (Tensor<Float>, Tensor<Float>) { ... } ``` -
rxwei revised this gist
Oct 21, 2018 . 1 changed file with 1 addition and 1 deletion.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -141,7 +141,7 @@ row in the matrix, which is exactly the </p> When this vector  represents the gradient of another function  at ), namely }), then the vector-Jacobian products will represent -
rxwei revised this gist
Oct 21, 2018 . 1 changed file with 7 additions and 5 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -59,11 +59,13 @@ maps points onto their corresponding slopes. In the context of Swift, differentiating a function `(Float) -> Float` produces `(Float) -> Float`. Functions with multiple arguments, such as `(Float, Float) -> Float`, can be thought of as a function whose input domain is a product of those arguments types, i.e. , so the derivative of such a function has type `(Float, Float) -> (Float, Float)`. According to this typing rule, the differential operator  can be declared as a higher-order function, overloaded for each number of arguments because a Swift function's argument list is not formally modeled as a tuple. ```swift func 𝒟<T: FloatingPoint>(_ f: (T) -> T) -> (T) -> T -
rxwei revised this gist
Oct 21, 2018 . 1 changed file with 28 additions and 17 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -46,8 +46,11 @@ programming language. ### Basic Calculus In basic calculus, differentiating a function of type  produces a function  that maps points onto their corresponding slopes. <p align="center"> <img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/9315f1516ee5847107808697e43693d91abfc6e8" @@ -80,18 +83,21 @@ func f(_ x: Double, _ y: Double) -> Double { In numerical computing, users often write code that operate on high-dimensional mathematical objects. The basic typing rules that we defined on real scalars (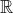) can be generalized for [module](https://en.wikipedia.org/wiki/Module_(mathematics))-like types such as vectors with extra consideration for shape. In vector calculus, the differentiation of a function  is defined per scalar because there are multiple inputs and multiple outputs. Full differentiation of vector-valued function  will result in a matrix, each of whose entries is a function that computes the partial derivative of an output scalar with respect to an input scalar. This matrix is called a [Jacobian](https://en.wikipedia.org/wiki/Jacobian_matrix_and_determinant). In this definition, the Jacobian matrix has type ^{mn}). For simplicity, we will model it as a function that maps vectors to real-valued matrices . <p align="center"> <img src="https://wikimedia.org/api/rest_v1/media/math/render/svg/74e93aa903c2695e45770030453eb77224104ee4" @@ -119,9 +125,11 @@ next, we discuss how Automatic Differentiation comes in the picture. ### Gradient and Reverse-Mode AD When we let a [one-hot](https://en.wikipedia.org/wiki/One-hot) row vector  left-multiply a Jacobian matrix of type , we are selecting one row in the matrix, which is exactly the [gradient](https://en.wikipedia.org/wiki/Gradient) of 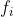 evaluated at 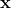, i.e. ). @@ -130,7 +138,8 @@ which is exactly the [gradient](https://en.wikipedia.org/wiki/Gradient) of <img src="https://latex.codecogs.com/gif.latex?\nabla{f_i}(\mathbf{x})=\mathbf{v}^i\mathbf{J_f}(\mathbf{x})=\bigg[\dfrac{\partial{f_i}(\mathbf{x})}{\partial&space;x_1}&space;\&space;\cdots&space;\&space;\dfrac{\partial{f_i}(\mathbf{x})}{\partial{x_n}}\bigg]" title="\nabla{f_i}(\mathbf{x})=\mathbf{v}^i\mathbf{J_f}(\mathbf{x})=\bigg[\dfrac{\partial{f_i}(\mathbf{x})}{\partial x_1} \ \cdots \ \dfrac{\partial{f_i}(\mathbf{x})}{\partial{x_n}}\bigg]" /> </p> When this vector  represents the gradient of another function  at ), namely }), then the vector-Jacobian products will represent @@ -165,8 +174,10 @@ partial derivatives from the final output, eventiually reaching each input. ### Directional Derivatives and Forward-Mode AD Similarly, when we let a column vector  right-multiply a Jacobian value matrix of type , the result is a vector whose elements are exactly the [directional derivatives](https://en.wikipedia.org/wiki/Directional_derivative) of each 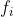 evaluated at 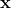 in direction . -
rxwei revised this gist
Oct 21, 2018 . 1 changed file with 3 additions and 3 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -127,7 +127,7 @@ which is exactly the [gradient](https://en.wikipedia.org/wiki/Gradient) of ). <p align="center"> <img src="https://latex.codecogs.com/gif.latex?\nabla{f_i}(\mathbf{x})=\mathbf{v}^i\mathbf{J_f}(\mathbf{x})=\bigg[\dfrac{\partial{f_i}(\mathbf{x})}{\partial&space;x_1}&space;\&space;\cdots&space;\&space;\dfrac{\partial{f_i}(\mathbf{x})}{\partial{x_n}}\bigg]" title="\nabla{f_i}(\mathbf{x})=\mathbf{v}^i\mathbf{J_f}(\mathbf{x})=\bigg[\dfrac{\partial{f_i}(\mathbf{x})}{\partial x_1} \ \cdots \ \dfrac{\partial{f_i}(\mathbf{x})}{\partial{x_n}}\bigg]" /> </p> When this vector `vⁱ` represents the gradient of another function `g: ℝᵐ → ℝ` at @@ -143,7 +143,7 @@ body of this function can be defined in terms of `𝒟`, the differential operat that returns a Jacobian. <p align="center"> <img src="https://latex.codecogs.com/gif.latex?\dfrac{\partial&space;g(\mathbf{f}(\mathbf{x}))}{\partial&space;\mathbf{x}}=\dfrac{\partial&space;g}{\partial&space;\mathbf{f}(\mathbf{x})}\mathbf{J_f}(\mathbf{x})&space;=&space;\bigg[&space;\dfrac{\partial&space;g(\mathbf{x})}{\partial&space;x_1}&space;\&space;\cdots&space;\&space;\dfrac{\partial&space;g(\mathbf{x})}{\partial&space;x_n}&space;\bigg]" title="\dfrac{\partial g(\mathbf{f}(\mathbf{x}))}{\partial \mathbf{x}}=\dfrac{\partial g}{\partial \mathbf{f}(\mathbf{x})}\mathbf{J_f}(\mathbf{x}) = \bigg[ \dfrac{\partial g(\mathbf{x})}{\partial x_1} \ \cdots \ \dfrac{\partial g(\mathbf{x})}{\partial x_n} \bigg]" /> </p> ```swift @@ -172,7 +172,7 @@ of each 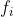 evaluated at 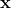 in direction . <p align="center"> <img src="https://latex.codecogs.com/gif.latex?\nabla_\mathbf{v}\mathbf{f}(\mathbf{x})=\mathbf{J_f}(\mathbf{x})\mathbf{v}=\bigg[\nabla_\mathbf{v}{f_1}(\mathbf{x})\&space;\cdots\&space;\nabla_\mathbf{v}{f_m}(\mathbf{x})\bigg]" title="\nabla_\mathbf{v}\mathbf{f}(\mathbf{x})=\mathbf{J_f}(\mathbf{x})\mathbf{v}=\bigg[\nabla_\mathbf{v}{f_1}(\mathbf{x})\ \cdots\ \nabla_\mathbf{v}{f_m}(\mathbf{x})\bigg]" /> </p> The linear function that takes a vector and right-multiplies the Jacobian value -
rxwei revised this gist
Oct 20, 2018 . 1 changed file with 84 additions and 15 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -1007,20 +1007,89 @@ Turns out, this is not a new problem - we should learning from how we deal with calling conventions in Swift. Functions with different calling conventions have different type signatures, e.g. `@convention(thick)` and `@convention(thin)`, and function convert back and forth through conversion thunks implicitly. ```swift // A "thin" function that captures no variables. // Its representation is `@convention(thin)` by default. func f(x: Int) { return x } var globalVar = 30 // A "thick" function that captures the value of `globalVar`. // Its representation is `@convention(thick)` by default. let g = { x in globalVar + x } // A higher-order function. // The closure argument `h`'s representation is `@convention(thick)`, because it should // be able to take closures that capture variables. func takeFunc(_ h: (Float) -> Float) { ... } takeFunc(f) // Implicitly converted function `f` to a `convention(thick)` closure by // creating a conversion thunk. takeFunc(g) // `g` is thick already. No conversion needed. ``` Sometimes, different conventions have different binary representations for storing captured variables and such, just like the example with `f` and `g` above. In AD, the only difference between a non-differentiable function and a differentiated function (say, in reverse mode) is whether the function carries a few other function pointers that represent the function's adjoint code, so we can model differentiable functions using a "thicker" function type, which bundles the original function representation along with pointers to the original function's Jacobian-vector product functions and/or vector-Jacobian product functions. When a normal function with a visible body gets passed as an `@autodiff` function, the function will be differentiated. ```swift // `f` is a normal function that has type `(Float) -> Float`. func f(x: Float) -> Float { return sin(x) } // `f` gets implcitly converted (or more accurately, differentiated). let g = f as @autodiff (Float) -> Float func takesFunc(_ someFunc: @autodiff (Float) -> Float) { #derivatives(someFunc) ... } // At the callsite of `takesFunc(_:)`, `f` gets implcitly differentiated to become // `@autodiff (Float) -> Float`. takesFunc(f) ``` If a normal function does not have a visible body, then it cannot be passed as an `@autodiff` function. Swift will show an error at compile-time. ```swift var normalFuncWithOpaqueBody: (Float) -> Float = ... takesFunc(normalFuncWithOpaqueBody) ``` ```console test.swift:19:11: error: function is not differentiable, but the contextual type is '@autodiff (Float) -> Float' takesFunc(normalFuncWithOpaqueBody) ^~~~~~~~~~~~~~~~~~~~~~~~ test.swift:17:4: note: value defined here var normalFuncWithOpaqueBody: (Float) -> Float = ... ^~~~~~~~~~~~~~~~~~~~~~~~ ``` At first glance, this could even be an addition to the existing `@convention` attribute as something like `@convention(autodiff)`, however, differentiability does not align semantically with `@convention`. First, when a function becomes its differentiable (or differentiated) form, its original calling convention is not changed. Second, functions with any convention is technically differentiable, including `thin`, `thick`, `method`, etc. Third, differentiability is not the only information that needs to be encoded -- there's also the order of differentiation. Therefore, we need a separate dimension of "thickness" in the function type: differentiability. We define a new formalization of differentiability in Swift's type system, including an `@autodiff` function type attribute, an extension to functions' @@ -1237,7 +1306,7 @@ As we can see, since we are to differentiate a higher-order function's argument (thanks to Generalized Differentiability), we can define `derivatives(of:)` and `gradient(of:)` as Swift functions in terms of more general raw differential operators, `#differential` and `#pullback`, to replace `#derivatives` and `#gradient`! These differential operators work seamlessly with closure captures, error-throwing functions, or arbitrary side-effecting code that do not @@ -1827,7 +1896,7 @@ Recall that the motivation of introducing a general, future-proof ```swift extension SGD { func fit(_ parameters: inout Parameters, gradients: Parameters) { parameters.update(withGradients: gradients) { θ, g in θ = θ.moved(toward: -θ.tangentVector(from: g) * learningRate) } } -
rxwei revised this gist
Oct 20, 2018 . 1 changed file with 10 additions and 5 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -100,7 +100,7 @@ we will model it as a function that maps vectors to real-valued matrices `J: ℝ While it is challenging to define this function with full type safety in Swift because shapes cannot be generic parameters yet, we can define a differential operator as the following, specialized on shapes. ```swift func 𝒟<T>(_ f: (Vector2<T>) -> Vector3<T>) -> (Vector2<T>) -> Matrix3x2<T> @@ -309,9 +309,9 @@ for (x, y) in minibatches { ### Full Extensibility: Custom Types and Derivatives We want our AD system to be fully extensible to the point where users can request derivatives of a function taking their own user-defined numeric types, and even use this feature to implement structure-dependent algorithms such as tree-recursive neural networks. Therefore, AD makes no assumptions about individual math functions or the types it should support. We enable library designers and developers to easily define any type or differentiable functions, all in pure Swift code. @@ -355,7 +355,12 @@ All differential operators are defined in Swift, and developers can create their own differential operators by composing existing ones. For example, the user can use the "forward-on-reverse" approach to compute [Hessian-vector products](https://en.wikipedia.org/wiki/Hessian_matrix), where the `hvp(at:in:)` operator is defined as a native Swift function. The [`@autodiff(order: 2)`](#the-autodiff-function-type-attribute) attribute in the closure type signature marks the closure argument as being differentiable up to at least the 2nd order, so that the caller of `hvp(at:in:)` will differentiate the actual closure argument as needed.so that the caller of this function will implicitly trigger differentiation as needed. ```swift func hvp<T: Differentiable, R: FloatingPoint>( -
rxwei revised this gist
Oct 20, 2018 . 1 changed file with 1 addition and 1 deletion.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -829,7 +829,7 @@ func g(_ x: Float) -> (Vector<Float>, Vector<Float>) { return x • w } #derivatives(g) // (Float) -> (Vector<Float>, Vector<Float>) ``` The grammar of these raw differential operators is defined as follows: -
rxwei revised this gist
Oct 20, 2018 . 1 changed file with 1 addition and 1 deletion.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -829,7 +829,7 @@ func g(_ x: Float) -> (Vector<Float>, Vector<Float>) { return x • w } #derivatives(f) // (Float) -> (Vector<Float>, Vector<Float>) ``` The grammar of these raw differential operators is defined as follows: -
rxwei revised this gist
Oct 20, 2018 . 1 changed file with 2 additions and 3 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -788,9 +788,8 @@ func adjointBar(_ x: Vector<Float>, y: Float, adjoint: Float) -> Vector<Float> { } ``` ```console test.swift:3:35: error: function `bar` does not support higher-order differentiation because its adjoint is not differentiable; would you like to add `once`? @differentiable(reverse, adjoint: adjointBar) ^~~~~~~~~~ test.swift:8:6: note: `adjointBar` is defined here -
rxwei revised this gist
Oct 20, 2018 . 1 changed file with 8 additions and 5 deletions.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -130,7 +130,7 @@ which is exactly the [gradient](https://en.wikipedia.org/wiki/Gradient) of <img src="https://latex.codecogs.com/gif.latex?\nabla{f_i}(\mathbf{x})=\mathbf{v}^i\mathbf{J_f}(\mathbf{x})=\bigg[\dfrac{\partial{f_i}(\mathbf{x})}{\partial&space;x_0}&space;\&space;\cdots&space;\&space;\dfrac{\partial{f_i}(\mathbf{x})}{\partial{x_n}}\bigg]" title="\nabla{f_i}(\mathbf{x})=\mathbf{v}^i\mathbf{J_f}(\mathbf{x})=\bigg[\dfrac{\partial{f_i}(\mathbf{x})}{\partial x_0} \ \cdots \ \dfrac{\partial{f_i}(\mathbf{x})}{\partial{x_n}}\bigg]" /> </p> When this vector `vⁱ` represents the gradient of another function `g: ℝᵐ → ℝ` at ), namely }), then the vector-Jacobian products will represent @@ -667,7 +667,7 @@ There are five options for differentiability: 5. Linear: `@differentiable(linear)` By definition, a linear map is always a unary function and its Jacobian is the matrix associated with this linear transformation itself. In other words, both its differential and its pullback are itself. @@ -715,7 +715,7 @@ As explained, differentiabilities have different functional requirements. 4. Other differentiabilities Other differentiabilities such as `constant` and `linear` do not require any associated functions. However, users can choose to specify tangent/adjoint function(s) for their own purposes such as custom optimizations. @@ -778,9 +778,12 @@ func bar(_ x: Vector<Float>) -> Float { return sin(x)[0] } var someGlobalVariable: Vector<Float> = [1, 1, 1] func adjointBar(_ x: Vector<Float>, y: Float, adjoint: Float) -> Vector<Float> { var ∂y∂x = Vector<Float>(repeating: 0, shape: x.shape) someGlobalVariable[0] = cos(x[0]) * adjoint ∂y∂x[0] = someGlobalVariable[0] return ∂y∂x } ``` @@ -1062,7 +1065,7 @@ due to code size. In order to make the system consistent, we make each Since we want to support differentiating opaque functions, we must support creating one. The fact is, the user does not even need to know about `@autodiff` or intentionally create differentiable functions if they are working with functions in the current module. Whenever a local function declaration gets used where the contextual type has an `@autodiff` attribute on it, Swift differentiates it. If differentiation fails, Swift reports an error at -
rxwei revised this gist
Oct 20, 2018 . 1 changed file with 1 addition and 1 deletion.There are no files selected for viewing
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode charactersOriginal file line number Diff line number Diff line change @@ -1430,7 +1430,7 @@ composition of the forward-mode differential operator and the reverse-mode differential operator on a function. <p align="center"> <img src="https://latex.codecogs.com/png.latex?\mathbf{H}_f(\mathbf{x})\mathbf{v}&space;=&space;\mathbf{J}_{\nabla&space;f}(\mathbf{x})\mathbf{v}" title="\mathbf{H}_f(\mathbf{x})\mathbf{v} = \mathbf{J}_{\nabla f}(\mathbf{x})\mathbf{v}" /> </p> Just like other differential operators, we can define the Hessian-vector
NewerOlder